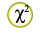Pearsonov hi-kvadrat test (ang. Pearson’s Chi-squared test) velja za zelo vsestransko statistično metodo, še posebej pri analizi opisnih spremenljivk. Gre za mero ujemanja, ki jo je razvil Karl Pearson.
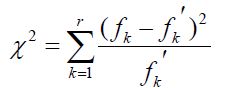
…kjer so fk dejanske/opazovane frekvence, fk’ pa pričakovane/teoretične frekvence.
Pearsonov hi-kvadrat test velja za originalni hi-kvadrat test, ne pa tudi edini. Marsikomu ni znano, da obstajajo še drugi hi-kvadrat testi. Pearsonov test uporabljamo za testiranje enake verjetnosti ali testiranje neodvisnosti dveh spremenljivk v kontingenčni tabeli.
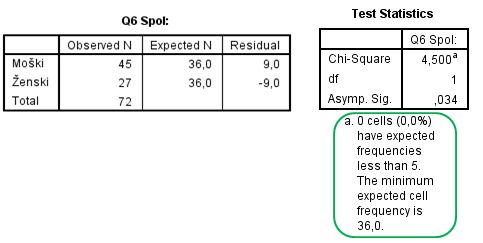
1. Test enake verjetnosti (ang. Chi-square Goodness-of-fit test) preverja ali so vsi odgovori enega vprašanja/spremenljivke enako pogosti (noben odgovor ne prevladuje) oz. ali je pogostost pri odgovorih različna (več respondenetov je označevalo en odgovor kot ostale). Postavimo ničelno in alternativno hipotezo:
- H0 = vsi odgovori so enako verjetni
- H1 = vsi odgovori niso enako verjetni (običajno se ta hipoteza sklada z raziskovalno hipotezo).
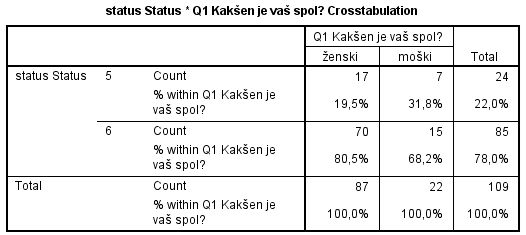
2. Test neodvisnosti (ang. Chi-square test for independence) preverja ujemanje dejanskih in pričakovanih frekvenc oz. odvisnost/povezanost med spremenljivkama. Postavimo ničelno in alternativno hipotezo:
- H0 = spremenljivki sta neodvisni/nepovezani
- H1 = spremenljivki sta odvisni/povezani (običajno se ta hipoteza sklada z raziskovalno hipotezo).
Na osnovi izračunane vrednosti hi-kvadrata in izbrane kritične vrednosti (običajno 0,05) bodisi sprejmemo H0 (kadar rezultat ni statistično značilen), bodisi zavrnemo H0 in z izbranim tveganjem sprejmemo H1 (kadar je rezultat statistično značilen).
Čeprav Pearsonov hi-kvadrat test velja za zelo vsestransko statistično orodje, pa pri predstavitvi rezultatov pogosto opažamo neupoštevanje njegove pomembne predpostavke. Za kakovostne rezultate mora biti izpolnjen en pogoj, in sicer: pričakovane frekvence ne smejo biti manjše od 5 (avtor pogoja je statistik William G. Cochran). Ker gre za zelo strog pogoj, ki velikokrat zapre nadaljnje možnosti raziskovanja, se v praksi uporablja nekoliko milejša oblika pogoja, in sicer: najvišji dovoljeni delež pričakovanih frekvenc manjših od 5 je 20 % in nobena med njimi ne sme biti manjša od 1.
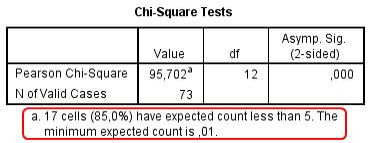
V praksi kršitev tega pogoja v fazi analize podatkov skušamo reševati na različne načine, kot so združevanje sorodnih kategorij odgovorov (kadar je to tudi vsebinsko smiselno), izločitev določene kategorije iz analize, uporaba nadomestnih testov, npr. hi-kvadrat test razmerij verjetnosti (ang. Likelihood Ratio Chi-square), Fisherjev natančni test (ang. Fisher’s exact test) ipd. Velikokrat se tudi zgodi, da pri analizi ni mogoča nobena kakovostna rešitev, zato izpostavljamo, da je pomembno imeti to predpostavko v mislih že v fazi načrtovanja raziskave in pripravi anketnega vprašalnika.
Imate dileme pri statistični analizi podatkov s hi-kvadrat testom? Pošljite nam vaše rezultate v pregled in svetovali vam bomo, kako naprej. Oglasite se: info@benstat.si